Rectas del Plano y Posiciones del Plano (2 en 1)

Rectas del Plano.

 

Posiciones del Plano.

Bisectriz ángulo mixtilíneo

Es aquel que determinan un arco y una recta concurrentes.

Nos dan el arco y la recta que corta al arco en el punto A.

Se traza la perpendicular a la recta por un punto cualquiera y se toman un número de partes con la misma medida.

Se trazan por estos puntos paralelas a la recta dada.

Dibujamos por el punto B del arco una semirrecta y trasladamos las medidas creadas en la perpendicular a la recta. El mismo número con la misma medida.
Haciendo los arcos concéntricos cortamos a las paralelas en unos puntos de intersección que determinan el resultado.
El resultado se traza a mano alzada o con una plantilla de curvas.

Este es un Applet de Java creado con GeoGebra desde www.geogebra.org – Java no parece estar instalado Java en el equipo. Se aconseja dirigirse a www.java.com

Recta que corta a otras 2 y pasa por un punto.

Trazoide es una Web de obligada visita para los estudiantes de Bachillerato y muy recomendable para el resto.

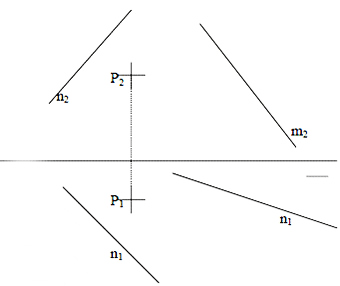En este caso necesitamos solucionar el problema de hallar una recta r que corta a otras 2 rectas (m y n) y pasa por el punto P.

Los pasos a seguir serían:

1. -Halla el plano P formado por la recta M y el punto P
2. -Halla el plano Q formado por la recta N y el punto P
3. -La recta R buscada es la intersección de P y Q

Para solucionar otros problemas similares en casos parecidos ¡atención a este índice!

ÍNDICE de los ejercicios de RECTAS QUE SE APOYAN EN OTRAS DOS

a.        Recta paralela a la línea de tierra y que se apoye en otras dos

b.        Recta paralela al plano vertical , que diste una distancia respecto del plano vertical y corte a otras dos  

c.        Recta perpendicular a otra por un punto y que corte además a otra recta

d.     Hallar la mínima distancia entre dos rectas, que se cruzan, con una pendiente conocida respecto del plano horizontal

e.     Hallar la mínima distancia entre dos rectas, que se cruzan, con una pendiente conocida respecto de una de ellas

f.        Hallar los puntos de una recta cuya mínima distancia a otra recta es una cantidad conocida

g.        Mínima distancia entre dos rectas que se cruzan

h.        Recta paralela a un plano y que se apoya en otras dos dadas

i.         Recta perpendicular a otras dos, una de ellas frontal

j.        Recta perpendicular a otras dos, una de ellas frontal

k.        Recta que se apoya en otras dos y pasa por un punto

l.         Recta que se apoya en otras dos y pasa por un punto

m.      Recta perpendicular a otras dos rectas que se cruzan, mediante cambios de plano

n.        Recta perpendicular a otras dos rectas que se cruzan, mediante giros

o.        Recta que se apoya en otras tres rectas y pasa por un punto de una de ellas

p.        Recta que se apoya en otra de perfil, pasa por un punto y corta a la línea de tierra

Otra versión de la historia:

Determinar una recta que se apoye en dos conocidas, R y S, y pase por un punto, P. 

SOLUCIÓN 

1 - Determinar un punto, X, cualquiera en la primera recta, R, y unirlo con el dado, P. Esto da una nueva recta, T. 

 2 - La primera recta, R, y la tercera (nueva), T, forman un plano (no hacen falta sus trazas). Hallar la dirección de la dirección de la traza del plano mediante una recta horizontal (paralela a la linea de tierra en cualquier sitio y donde las corte se bajan y se unen). 

 3 - Hallar la intersección entre el plano (formado por la primera y tercera recta, R y T) con la segunda recta, S. Para ello hacer un cambio de plano (segunda linea de tierra perpendicular a la dirección de la traza del plano), cambiar los puntos de una recta (la R o la T) y cambiar la segunda recta, S, donde esta, corte a la otra (punto Y) es la intersección. Llevarlo a las otras proyecciones de S mediante perpendiculares a las lineas de tierra. 

 4 - Unir el punto intersección, Y, con el dado, P y se obtiene la recta buscada

Igualdad de figuras planas.

Bisectriz ángulo curvilíneo

Es el que determinan dos arcos que son concurrentes en un punto.

Nos dan dos arcos de radio arbitrario con centros en O1 y O2.

Se trazan semirrectas partiendo de los centros de los arcos. Se dividen en un número determinado de partes iguales en ambas.

Con centro en O1 y O2 se trazan arcos concéntricos que pasan por las divisiones.

Las intersecciones de dos arcos correspondientes a la misma división determinan los puntos de la bisectriz curvilínea.

Este es un Applet de Java creado con GeoGebra desde www.geogebra.org – Java no parece estar instalado Java en el equipo. Se aconseja dirigirse a www.java.com

Apuntes de Transformaciones Geométricas

 

Para completar lo que vemos en clase, para consultar en caso de duda, por si tenemos interés, para buscar la solución a los ejercicios de clase o si queremos llevar la asignatura un poco más allá de la preparación de la Selectividad.

Extraído de un libro de texto y unos apuntes encontrados en la Web.

TRANSFORMACIONES GEOMÉTRICAS: Proyectividad y Homografía, Homología y Afinidad, Inversión.

Apuntes de Homología: