Recta que corta a otras 2 y pasa por un punto.

Trazoide es una Web de obligada visita para los estudiantes de Bachillerato y muy recomendable para el resto.

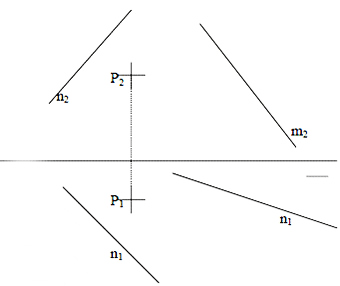En este caso necesitamos solucionar el problema de hallar una recta r que corta a otras 2 rectas (m y n) y pasa por el punto P.

Los pasos a seguir serían:

1. -Halla el plano P formado por la recta M y el punto P
2. -Halla el plano Q formado por la recta N y el punto P
3. -La recta R buscada es la intersección de P y Q

Para solucionar otros problemas similares en casos parecidos ¡atención a este índice!

ÍNDICE de los ejercicios de RECTAS QUE SE APOYAN EN OTRAS DOS

a.        Recta paralela a la línea de tierra y que se apoye en otras dos

b.        Recta paralela al plano vertical , que diste una distancia respecto del plano vertical y corte a otras dos  

c.        Recta perpendicular a otra por un punto y que corte además a otra recta

d.     Hallar la mínima distancia entre dos rectas, que se cruzan, con una pendiente conocida respecto del plano horizontal

e.     Hallar la mínima distancia entre dos rectas, que se cruzan, con una pendiente conocida respecto de una de ellas

f.        Hallar los puntos de una recta cuya mínima distancia a otra recta es una cantidad conocida

g.        Mínima distancia entre dos rectas que se cruzan

h.        Recta paralela a un plano y que se apoya en otras dos dadas

i.         Recta perpendicular a otras dos, una de ellas frontal

j.        Recta perpendicular a otras dos, una de ellas frontal

k.        Recta que se apoya en otras dos y pasa por un punto

l.         Recta que se apoya en otras dos y pasa por un punto

m.      Recta perpendicular a otras dos rectas que se cruzan, mediante cambios de plano

n.        Recta perpendicular a otras dos rectas que se cruzan, mediante giros

o.        Recta que se apoya en otras tres rectas y pasa por un punto de una de ellas

p.        Recta que se apoya en otra de perfil, pasa por un punto y corta a la línea de tierra

Otra versión de la historia:

Determinar una recta que se apoye en dos conocidas, R y S, y pase por un punto, P. 

SOLUCIÓN 

1 - Determinar un punto, X, cualquiera en la primera recta, R, y unirlo con el dado, P. Esto da una nueva recta, T. 

 2 - La primera recta, R, y la tercera (nueva), T, forman un plano (no hacen falta sus trazas). Hallar la dirección de la dirección de la traza del plano mediante una recta horizontal (paralela a la linea de tierra en cualquier sitio y donde las corte se bajan y se unen). 

 3 - Hallar la intersección entre el plano (formado por la primera y tercera recta, R y T) con la segunda recta, S. Para ello hacer un cambio de plano (segunda linea de tierra perpendicular a la dirección de la traza del plano), cambiar los puntos de una recta (la R o la T) y cambiar la segunda recta, S, donde esta, corte a la otra (punto Y) es la intersección. Llevarlo a las otras proyecciones de S mediante perpendiculares a las lineas de tierra. 

 4 - Unir el punto intersección, Y, con el dado, P y se obtiene la recta buscada