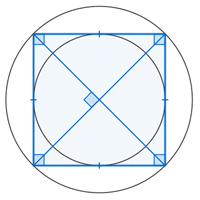
Divaguemos un poco en torno al cuadrado, y supongamos que no sabemos cómo se define precisamente. Esto nos llevaría a considerar varias propiedades que se cumplen en un cuadrado cualquiera, por ejemplo:
1. Sus lados son congruentes
2. Sus lados son paralelos
3. Sus ángulos internos son todos congruentes
4. Tiene sólo ángulos rectos
5. Sus diagonales son perpendiculares
6. Sus diagonales se dimidian
7. Es inscriptible
8. Es circunscriptible
9. Las circunferencias inscrita y circunscrita son concéntricas
10. Sus ángulos opuestos y adyacentes son congruentes
2. Sus lados son paralelos
3. Sus ángulos internos son todos congruentes
4. Tiene sólo ángulos rectos
5. Sus diagonales son perpendiculares
6. Sus diagonales se dimidian
7. Es inscriptible
8. Es circunscriptible
9. Las circunferencias inscrita y circunscrita son concéntricas
10. Sus ángulos opuestos y adyacentes son congruentes
*-Busca el significado de:Dimidiar, congruente (lado y ángulo), inscribir y circunscribir.
*-De las 10 propiedades ¿con cuales te quedarías para definir de forma sencilla y precisa al cuadrado?
*-Haz una clasificación, aplicando el criterio anterior, de todos los cuadriláteros menos del trapezoide.
En esta escena, es posible articular de manera práctica el concepto de cuadrado como la intersección entre los conceptos de rectángulo y rombo.
En el primer caso se tiene un rectángulo, en el que el ángulo que forman las diagonales se puede ajustar moviendo el punto R. Si se logra que las diagonales sean perpendiculares, se puede observar que como consecuencia los lados se hacen todos congruentes, es decir, se obtiene un cuadrilátero equiángulo y equilátero como es el cuadrado.
Análogamente, en el caso 2 se tiene un rombo, construido como un cuadrilátero equilátero. Si se ajusta C para que al menos un ángulo interno sea recto, se puede observar cómo el rombo se convierte en un cuadrado.